For a full chronological publication list, please click here: publication list
Broad Research Areas and Techniques:
- Applied Mathematics & Applied Analysis
- Differential Equations & Dynamical Systems
- Probability & Stochastic Analysis
- Scientific Computing & Numerical Analysis
- Networks & Complex Systems
- Applications in the Sciences & Engineering
- ... and particularly the interfaces between the above fields!
Main Research Topics:
- Multiscale Dynamics
- Stochastic Dynamics
- Network Dynamics
- PDE & Nonlocal Dynamics
- Numerical Dynamics
- Applications in the Biosciences
- Applications in Physics
|
|
Multiscale Dynamics:
| 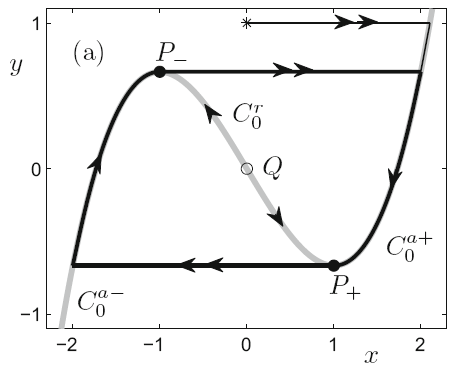 |
Stochastic Dynamics:Many
dynamical models,
particularly those arising in applications, are incomplete. One often
misses small-scale or finite-size intrinsic
effects as well as external disturbances and environmental
fluctuations. Therefore, using a stochastic dynamics approach provides
a good compromise to keep modelling complexity tractable but
to still capture important effects and phenomena. There are many
different approaches to stochastic systems, and usually one finds that
a mixture of techniques is the most powerful strategy to analyze a
given
problem. Examples of such techniques are direct sample path estimates
providing fine scale estimates, probability distribution methods
connecting to partial differential equation theory, focusing on
stochastic effects (metastability, large deviations,
stochastic/coherence resonance, isochronicity, etc), abstract random
dynamical systems approaches, and specialized numerical methods for
stochastic dynamics. Furthermore, models from applications as well as
data-driven approaches naturally involve the challenge to deal
with noise. My work in the area of stochastic dynamics is driven
by constructing an applicable, yet mathematically generic, theory that
focuses on dynamics near instability.
Focus directions and results: - development of early-warning sign theory for (stochastic) bifurcations [J7,J17,J1,J21,J26,J30,J45,J46,J95,J121] - new fast-slow stochastic theory and stochastic mixed-mode oscillations [J10,J25,J42,J64,J82] - effects and concepts: steady-state resonance, quenced resonance, RDS isochrons [J11,J42,J81,J115] - designing stochastic numerical continuation and rigorous validation methods [J13,J31,J38,J54,J68] - pattern formation and travelling waves for SPDEs [J15,J21,J31,J50,J51,J65,J73,J105,C2,J113,J133] - large deviations and gradient flows for stochastic neural field models [J18,J59] - stochastic differential equation dynamics via rough paths and regularity structures [J33,J40,J86,J118] - new methods for random differential equations and bifurcations [J42,J62,J69,J91,J108,J139] - solution theory and dynamics for quasilinear SPDEs [J33,J70,J75,C2,J79] Online Talk: "Exploring Bifurcations of Stochastic PDEs", 07.09.2021, ICMS Diffusive Systems Online Talk: "Rough Center Manifolds", 08.11.2021, Stochastics Seminar Uni Leipzig Online Talk: "Mathematical Foundations of Early-Warning Signs and Resilience", 09.08.2022, Lorenz Center Leiden Online Talk: "Mathematical Foundations of Early-Warning Signs", ClimTip Seminar, 04.07.2024 Online Talk: "Stochastic Waves", 16.11.2022, UBC Mathematical Biology Seminar | 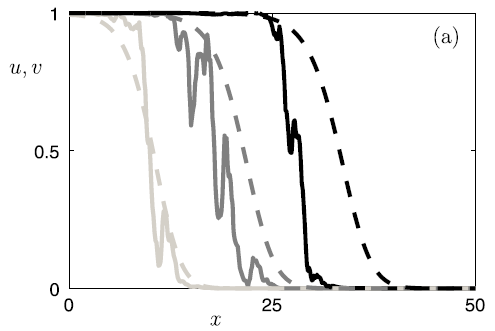 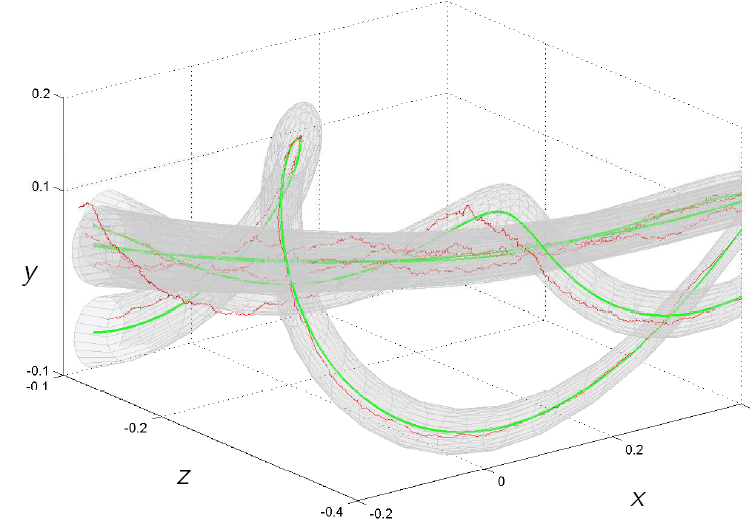 |
Network Dynamics:Networks
are ubiquitous:
The world around us is composed of individual parts, which interact.
This is true on all levels - whether in physics, chemistry, biology,
mathematics, engineering, epidemiology, technology, politics or
economics. Structure and collective behaviour emerges from the
properties of the individual parts and from the laws of their
interaction. Many breakthrough results have been obtained in the study
of networks but dynamics on and of networks is still relatively poorly
understood, particularly when considering the gaps between theory and
applications. Many dynamical systems posed on finite, but very large,
networks are virtually impossible to treat by pen-and-paper methods.
Hence, one has to employ mathematical techniques such as multiscale
reduction, symmetry arguments, moment closure, or infinite-network
limits. The analytical results must then be compared to numerical
simulations. These ideas naturally link network dynamics to the other
areas of my research, e.g., microscopic stochastic network dynamics
often leads to macroscopic local or nonlocal differential equation
models.
Focus directions and results: - dynamical effects in adaptive network dynamics [J11,J26,J49,J55,J72,J78,J101,J115,J119,J120] - mean-field and continnum limit differential equations [J58,J71,J93,J106,J112,J114] - stability, bifurcations, patterns, and warning signs for network dynamics [J19,J26,J49,J129,J131] - moment methods and generating function approaches [J61,J88,C1,J128] - higher-order interactions in network dynamics [J66,J74,J78,J98,J99,J110,J117,J132,J134] Online Talk: "Adaptive Epidemic Network Dynamics", 24.08.2021, Dynamics Days Europe Online Talk: "Mean-Field Limits of Network Dynamics", 29.09.2021, DMV/ÖMG Annual Meeting Online Talk: "A Universal Route to Explosive Phenomena", 08.01.2022, Dynamics Days US Online Talk: "Dynamics of Adaptive Higher-Order Networks", 14.06.2022, NORDITA Online Talk: "Dynamics on Neural Networks", 20.09.2024, IMS at NUS |  |
PDE & Nonlocal Dynamics:Based upon a
well-grounded understanding of dynamical systems on finite-dimensional
state spaces given by ordinary differential equations (ODEs), a next
natural step is to also consider partial differential equations (PDEs).
These equations arise often very naturally if spatial dependence of
physical processes, e.g., diffusion or advective transport, are taken
into account. Furthermore, many network dynamics models, such as
mean-field or continuum limits, also lead to models beyond ODEs,
frequently given by operator equations. The first mathematical task is
to derive these new dynamical systems from microscopic first
principles, and prove the existence and regularity of solutions. Yet,
from the viewpoint of applications, existence of solutions is only a
very first step as the models have derived to help us in the
understanding of new dynamical phenomena. As an example, one often
wants to understand pattern formation such as wave motion or the spatial structure of long-term steady states.
Focus directions and results: - travelling waves for the deterministic (local and nonlocal) PDEs [B2,J2,J5,J23,J29,J36,J83,J96,J102,C3] - pattern formation and travelling waves for SPDEs [J15,J37,J50,J65,J73,J90,J105,J113,J133] - large deviations and gradient flows for stochastic neural field models [J18,J59] - stationary and weakly-nonlinear patterns in (nonlocal) PDEs [B2,J22,J52,J47,J77,J104] - geometric fast-slow PDEs theory [J87,J97,J126,J130,J137,J138,J140] Online Talk: "Mean-Field Limits of Network Dynamics", 29.09.2021, DMV/ÖMG Annual Meeting Online Talk: "Geometric Singular Perturbation Theory for Fast-Slow PDEs", 04.02.2022, DCN Seminar Erlangen Online Talk: "Stochastic Waves", 16.11.2022, UBC Mathematical Biology Seminar Online Talk: "Towards GSPT for PDEs", 29.11.2022, BIRS Workshop | 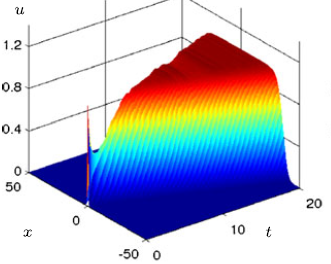 |
Numerical Dynamics:There are evidently many practical limits to purely analytical calculations in dynamical systems.
Local nonlinear theory is already challenging, and global extensions are possible if one has additional
exploitable structure e.g. multiple spatial scales, symmetry, energy
conservation, or multiple time scales. Yet, general global nonlinear phenomena
are frequently just accessible via numerical methods. A first step are
usually forward simulation algorithms, which efficiently and accurately
produce individual trajectories of dynamical systems. In many cases,
very robust and well-established simulation methods exist but it can
still be extremely difficult to understand the behaviour from just
having access to sample paths. My research goal in numerical dynamics
is to contribute to tailor-made numerical methods to provide access
more directly to critical objects in the study of nonlinear dynamics.
This includes the computation of invariant manifolds, improving and
extending numerical continuation methods for parametric studies, as
well as uncovering patterns numerically.
Focus directions and results: - computation of saddle slow manifolds and multiscale/singular bifurcation diagrams [J2,J3,J4,J5,J12,J63,J76] - designing stochastic numerical continuation methods [J13,J31,J38,J68] - computation of patterns in various PDEs and extending continuation methods [J28,J67,J77,J80,C3] - computational methods for random differential equations and uncertainty quantification [J69,J139] - simulation of multiscale / stochastic / network / nonlocal dynamics [J8,J11,J21,J23,J26,J43,J44,J66,J72,J83,J94,J111] Online Talk: "Continuation Methods for Biological Systems", 29.11.2021, Uni Iowa MathBio Seminar Online Talk: "Dynamical Systems for Deep Neural Networks", 25.07.2022, Applied Geometry Conference | 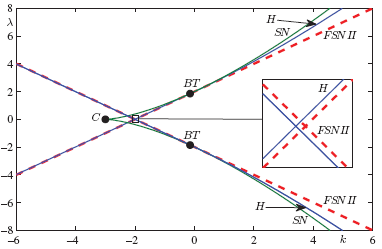 |
Applications in the Biosciences:The
biosciences are a
source of a wide variety of interesting dynamical problems since
complexity of biological systems is staggering, and their immediate
impact on our lives (e.g. epidemic spreading, ecological diversity,
systemic human diseases) is enormous. In
my
work, I have focused on problems in ecology, epidemiology, and
neuroscience. In all three areas, I have been mostly interested in
biological systems exhibiting interesting bifurcations and transitions
upon parameter variation. In particular, generic dynamical systems
methods are particularly
well-suited to classify, comprehend and exploit parameter dependencies
in biology as most models come with many, potentially even
stochastically varying, parameters. Typical systems with many important
parameters occur in the study of epidemic outbreaks, the death of
species, or the
onset of bursting/spiking behaviour in neurons. The methodology used
in my work on biological problems regularly combines different
mathematical approaches outlined above as biological systems are often
multiscale, stochastic, networked, and/or spatially structured.
Focus directions and results: - studying epidemic dynamics and its transitions [J17,J26,J34,J49,J76,J88,J101,J109,J119] - bifurcations and scaling in epileptic seizures and neuron dynamics [J5,J9,J24,J85,J115] - generalized models and periodic ecological dynamics [J13,J14,J16,J43] - modern biocomplexity modelling (stress, cliodynamics, public transport, etc.) [J84,J125,J135] - resilience: concepts and applications [J123] Online Talk: "Adaptive Epidemic Network Dynamics", 24.08.2021, Dynamics Days Europe Online Talk: "Continuation Methods for Biological Systems", 29.11.2021, Uni Iowa MathBio Seminar Online Talk: "Dynamics of Adaptive Higher-Order Networks", 14.06.2022, NORDITA Online Talk: "Mathematical Foundations of Early-Warning Signs and Resilience", 09.08.2022, Lorenz Center Leiden | 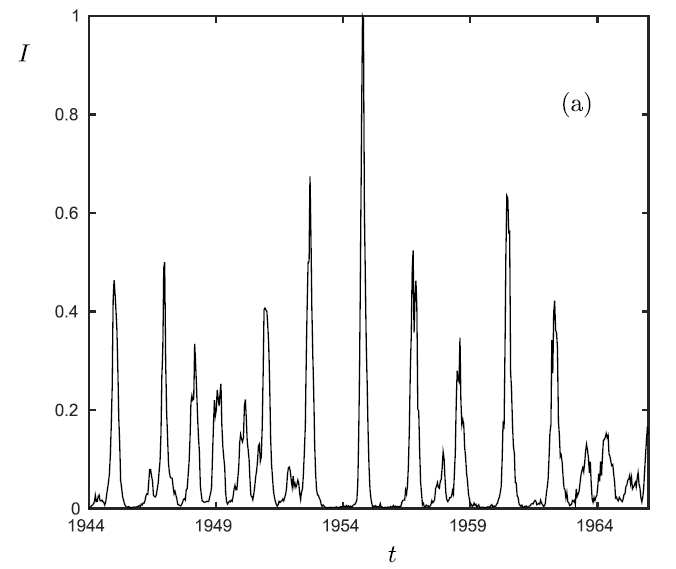 |
Applications in Physics:Similar
to the
biosciences (and historically far earlier), physical problems are
deeply integrated in the
science of nonlinear dynamical systems via providing key motivating
examples. In addition, from a theoretical viewpoint, many areas in
physics are highly interactive methodologically with a mathematical
dynamics perspective e.g.
statistical physics, biophysics, quantum physics, econophysics, just to
name a few. In
my work, I focus on macroscopic problems in physics, i.e.,
theoretical physics above quantum, atomic or molecular scales. A
typical research area, where macroscale effects are crucial is fluid
dynamics since the motion of many fluids is well-described by
differential equations. In relation
to this area, there has been an important recent surge of interest in
climate dynamics, and large parts of my recent
physics-driven research center around taming mathematical challenges
arising in climate science. Mathematical techniques are particularly
important in studying climate change as it basically impossible to just
run experiments, and even numerical simulations of large climate models
tend to be expensive and highly parametrized.
Focus directions and results: - early-warning signs, stochastic computation and dimension reduction for climate dynamics [J17,J35,J38,J64,J95,J100,J108,J116,J141] - data analysis of networks and robustness indicators of bifurcation scalings [J19,J26,J30] - particle-surface interaction in fluid dynamics, particle cluster formation, turbulence [J44,J57,J102] - resilience: concepts and applications [J123] Online Talk: "A Universal Route to Explosive Phenomena", 08.01.2022, Dynamics Days US Online Talk: "Mathematical Foundations of Early-Warning Signs and Resilience", 09.08.2022, Lorenz Center Leiden Online Talk: "Mathematical Foundations of Early-Warning Signs", ClimTip Seminar, 04.07.2024 | 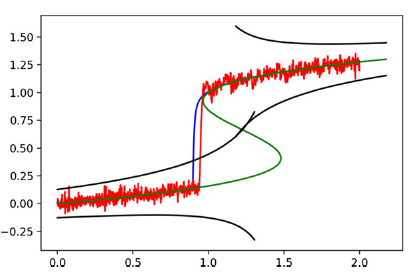 |